Pasos para trabajar en ATLAS.ti y un ejemplo de red construida

ATLAS.ti by selenia on Scribd

Infografia del método cuantitativo

tabla de contingencias: estadísticos SPSS ( chi- cuadrado, correlaciones y coeficiente de incertidumbre)

CHI- CUADRADO









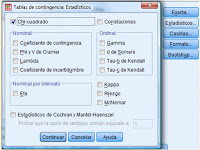
Es una prueba no paramétrica de comparación de proporciones para dos y más de dos muestras independientes, debe cumplir las siguientes características: • Los datos se ajustan a la distribución de chi cuadrada • Nivel nominal de la variable dependiente • Su función es comparar dos o más de dos distribuciones de proporciones y determinar que la diferencia no se deba al azar (que las diferencia sea estadísticamente significativa). 


La prueba del Chi Cuadrado es apropiada cuando los datos obtenidos en su estudio son de nivel nominal. Esto significa que en lugar de poder medir los puntajes de los sujetos, sólo es posible asignar los sujetos a una o más categorías. Esta medida no es propiamente una medida de asociación pero permite a partir de la idea que se puede definir "una asociación cero" en términos de la igualdad lograda entre la frecuencias observadas y las frecuencias esperadas. 

Nota Metodológica: Para calcular la medida de Chi-Cuadrado se sigue el siguiente procedimiento: el valor de la frecuencia esperada en cada celda de la matriz de una tabla de un cruce de variables es restado del valor de la frecuencia observada en esa celda y el valor resultante elevado al cuadrado.


CORRELACIONES 

El concepto de relación o correlación entre dos variables se refiere al grado de parecido o variación conjunta existente entre las mismas.Una relación lineal positiva entre dos variables X e Y significa que los valores de las dos variables varían de forma parecida: los sujetos que puntúan alto en X tienden a puntuar alto en Y y los que puntúan bajo en X tienden a puntuar bajo en Y. Una relación lineal negativa significa que los valores de ambas variables varían justamente el revés. La forma más directa de formarse una primera idea sobre el tipo de relación existente entre dos variables cuantitativas es a través de un Diagrama de dispersión. Este tipo de diagramas puede obtenerse mediante: Gráficos.

Correlaciones que incluye tres opciones (1) Bivariadas, para el estudio de la relación entre dos variables cuantitativas, (2) Parciales, para el estudio de la relación entre dos variables cuantitativas cuando se controla o elimina el efecto de terceras variables y (3) Distancias, para el estudio de la relación entre dos variables cualesquiera que sea su nivel de medida. 

COEFICIENTE DE INCERTIDUMBRE

Capacidad predictiva y de disminución del error de dicha predicción.La expresión de estos coeficientes depende de toda la distribución y no sólo de los valores modales, por lo que sólo toma el valor 0 en casos de total independencia. Ésta es su ventaja respecto a lambda, pero es más difícil de interpretar. Oscila entre 0 y 1. Posee dos versiones asimétricas (dependiendo de cuál de las dos variables se considera independiente) y una simétrica (cuando no se hace distinción entre variable dependiente e independiente).

COMO AGRUPAR DATOS EN SPSS

Datos descriptivos y gráficos de la población con rezago educativo de 15 años y más del INEGI

Datos descriptivos del INEGI de selenia ruiz perez

PROGRAMA SPSS

Análisis de los datos

Para poder obtener las cantidades que se muestran en los cuadros anteriores, se realizaron dos preguntas de tipo cuantitativo en el salón de clases del 7°B. 

Se utilizo el  programa SPSS y la información  obtenida de las preguntas como ejemplo para encontrar los resultados de nuestra estadística descriptiva, en los  cuadros anteriores se muestran la siguiente información: 

• media
• máximo
• mínimo
• rango
• número total
• desviación estándar
• varianza

Las preguntas fueron aplicadas a 23 compañeros del salón, lo cual los resultados obtenidos muestran que la mayoría utiliza el celular en horas de clases, visto como un distractor  para sus procesos de aprendizajes y solo una mínima parte no lo utiliza, en la otra pregunta se observa que la mayoría  no utiliza colectivo para llegar a la escuela, una media de la población utiliza un colectivo.

Corroborando los resultados obtenidos con un máximo de 3 y un mínimo de 1. con una media estándar de .152 y .159, una desviación estándar de .728 y . 765.

con una varianza de .530 y . .585. estos son los resultados obtenidos de dicha encuesta cuantitativa. 

 

   

Prezi

presentación en prezi sobre el tema " medidas de tendencia central de dispersión y distribución"

MAPA EN GOCONQR

métodos en la investigación científica 

Mapa Mental creado con GoConqr por selenia Ruíz Pérez

DIAGRAMA DE GANTT

Cronograma de actividades

Estadística descriptiva

La estadística descriptiva

La estadística descriptiva es la rama de las Matemáticas que recolecta, presenta y caracteriza un conjunto de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela, temperatura en los meses de verano, etc.) con el fin de describir apropiadamente las diversas características de ese conjunto.

 Al conjunto de los distintos valores numéricos que adopta un carácter cuantitativo se llama variable estadística.

 Las variables pueden ser de dos tipos: 

• Variables cualitativas o categóricas: no se pueden medir numéricamente (por ejemplo: nacionalidad, color de la piel, sexo).

 • Variables cuantitativas: tienen valor numérico (edad, precio de un producto, ingresos anuales). 

Las variables también se pueden clasificar en: 

• Variables unidimensionales: sólo recogen información sobre una característica (por ejemplo: edad de los alumnos de una clase). 

• Variables bidimensionales: recogen información sobre dos características de la población (por ejemplo: edad y altura de los alumnos de una clase).

 • Variables pluridimensionales: recogen información sobre tres o más características (por ejemplo: edad, altura y peso de los alumnos de una clase).  

 Los componentes de una estadística descriptiva 

MEDIA ARITMÉTICA:

La media aritmética de n valores, es igual a la suma de todos ellos dividida entre n . Se denota por x.

Las características de la media aritmética son: 

 1. Es una medida totalmente numérica o sea sólo puede calcularse en datos de características cuantitativas. 

2. En su cálculo se toman en cuenta todos los valores de la variable.

 3. Es lógica desde el punto de vista algebraico.

 4. La media aritmética es altamente afectada por valores extremos. 

5. No puede ser calculada en distribuciones de frecuencia que tengan clases abiertas. 

6. La media aritmética es única, o sea, un conjunto de datos numéricos tiene una y sólo una media aritmética. 

MEDIANA:

 La mediana es el punto central de una serie de datos ordenados de forma ascendente o descendente. 

De acuerdo al número de casos o datos, hay dos formas para calcular la mediana: para número impar y para número par: 

 • Número impar de datos ordenados de menor a mayor o de mayor a menor: la mediana es el valor que queda justo al centro. 

Ejemplo. Obtener la mediana de los siguientes datos: 4, 7, 1, 9, 2, 5, 6. 

Solución. Ordenando de forma ascendente: 1, 2, 4, 5, 6, 7, 9. El valor que queda al centro es el 5, porque hay tres datos antes y tres datos después de él, entonces la mediana es 5.

 Las características de la mediana son: 

1. En su cálculo no se incluyen todos los valores de la variable. 

2. La Mediana no es afectada por valores extremos.

 3. Puede ser calculada en distribuciones de frecuencia con clases abiertas. 4. No es lógica desde el punto de vista algebraico.  

MODA:

 La moda de un conjunto de datos numéricos es el valor que más se repite, es decir, el que tiene el mayor número de frecuencias absolutas. La moda puede ser no única e inclusive no existir.

 La moda es una medida de tendencia central muy importante, porque permite planificar, organizar y producir para satisfacer las necesidades de la mayoría. 

Ejemplo. Obtener la moda de los siguientes datos: -3, 3, -2, 0, 3, -1, -2, 4, 5, -2, 0, 1.

 Solución. Ordenando de forma ascendente: -3, -2, -2, -2, -1, 0, 0, 1, 3, 3, 4, 5. El valor que más se repite es el -2, por lo tanto ese valor es su moda.

 Ejemplo. Obtener la moda de los siguientes datos: 6, 2, -1, -5, 3, -3, -2, 5, 0, -4, 4, 1.

 Solución. Ordenando de forma ascendente: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6. Ningún valor se repite es, decir su moda no existe. 

 Las características de la moda son:

 1. En su cálculo no se incluyen todos los valores de la variable.

 2. El valor de la moda puede ser afectado grandemente por el método de designación de los intervalos de clases. 

3. No está definida algebraica mente. 

4. Puede ser calculada en distribuciones de frecuencia que tengan clases abiertas. 5. No es afectada por valores extremos. 

CONTAR:

Es una función que se utiliza para determinar el numero total de elementos que contiene un conjunto, cuyos contenidos sean números o una representación de un numero. 

DESVIACIÓN ESTÁNDAR

 La desviación estándar o desviación típica se define como la raíz cuadrada de los cuadrados de las desviaciones de los valores de la variable respecto a su media. 

La desviación estándar es una medida estadística de la dispersión de un grupo o población. Una gran desviación estándar indica que la población esta muy dispersa respecto de la media. Una desviación estándar pequeña indica que la población está muy compacta alrededor de la media. Para el caso de datos agrupados.

MÍNIMO: Se utiliza para encontrar  el valor más pequeño del conjunto de datos. Ejemplo:

 La edad más mínima que hay en el grupo de estudiantes es de 14 años.

 MÁXIMO:  Se utiliza para encontrar el dato de mayor valor que se presenta.Ejemplo:

 La edad máxima que hay en el grupo de estudiantes es de 18 años.

SUMA: Es el resultado de la suma de los valores del conjunto de datos.ejemplo:

 El total de las edades del grupo de estudiantes es de 154 

Bibliografías:

González, A,  F. (2006). Estadística descriptiva: Métodos Estadísticos Aplicados a las Auditorías Sociolaborales. Universidad de Cádiz.

Encuesta Likert sobre el clima frío

Encuesta likert sobre el frío by selenia on Scribd

RESULTADO DE LA ENCUESTA ( Cuantitativa)

Encuestas

 imágenes de primera actividad basada en la realización de una encuesta con preguntas cualitativas y cuantitativas.

ANALÍTICAS DE APRENDIZAJE

Ensayo que habla sobre el tema de " analítica del aprendizaje", basado en el vídeo realizado por el gabinete de tele- educación de la universidad politécnica de Madrid, impartido por el profesor Ángel fidalgo.

Analiticas Del Aprendizaje. by selenia on Scribd

Para los que deseen ver el vídeo sobre analíticas del aprendizaje, aquí se encuentra.